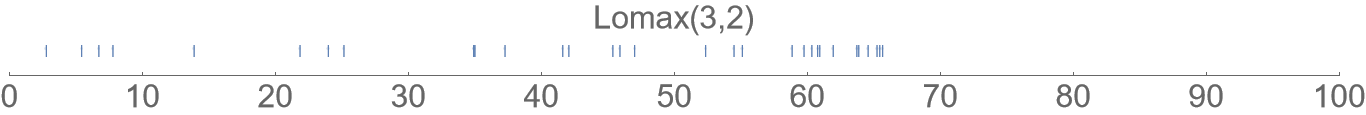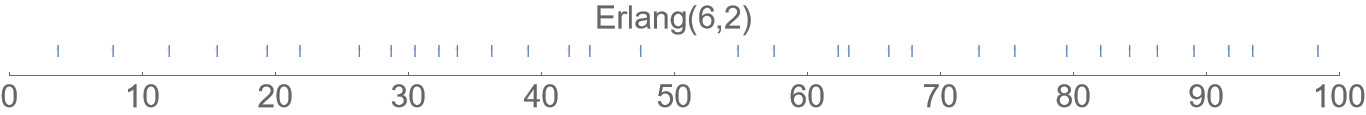Modelling event waiting times
In this article, I discuss some answers to the question: How do we model probabilistically the waiting time to the next event?
A textbook example where we want to model this is the time until a device fails. This happens some uncertain time in the future. This is assumed to happen repeatedly, and we should thous analyze this and prepare resources accordingly to be able to replace or fix the devices. Another practical example comes from commerce where we may want to analyze how to probabilistically express the waiting time until next customer purchase which may help with optimizing amount of products stored. But ultimately, at the lowest level of any time series are some timestamps of events, and we may when the next event is likely to happen. (Note: Time series are often understood as pre-aggregated representations such as the number of events of per day, but I’ll get to that later. I want to present these ideas in a bottom-up order starting from the lowest level.)
Independent & identically distributed
For the sake of mathematical simplicity, we here assume the events to be I.I.D. However, this may not always be accurate: For example in e-commerce, we may expect more frequent purchases during daytime than nighttime. Or the purchases of a certain product may be subject to a yearly seasonality or there are popularity trends. Accounting for this requires a more sophisticated models. However, keep in mind that even in the presence of such changes, they will usually be continuous and thus the I.I.D. assumption could be reasonable at least locally (i.e. short-term).
Memorylessness – Exponential & Geometric
A relatively simple, yet powerful assumption we may want to make about the process is memorylessness.
We call a probability distribution to be memoryless when the time already spent waiting for an event does not affect how much longer we need to wait for the next one to occur.
More formally, this is written as
\[\begin{equation} \label{eq:memoryless_definition} P(Y > t+s | Y \ge t)=P(Y > s) \end{equation}\]for the random variable $Y$ describing the waiting time between events, where $t\ge0$ can be interpreted as time already waited and $s\ge0$ as time yet to wait.
Let’s consider when this is justifiable. A customer not caring about how long ago the previous customer purchased something seems like a reasonable assumption and the memorylessness assumption may be appropriate. However, with the device example, it’s the case for a lot of devices to increase the chance of failure as they’re wearing off due to use and the memorylessness assumption may not be a suitable approximation anymore.
It can be shown rigorously (proof on Wikipedia), that for continuous time $t \in \mathbb{R}^+$, the memomoryless distribution needs to have density
\[\begin{equation}\label{eq:memoryless_distribution} p(t|\lambda) \propto e^{-\lambda t} \end{equation}\]for some parameter $\lambda \in \mathbb{R}^+$. This is of course the exponential distribution.
The idea of the proof is to rewrite (using conditional probability definition) the memorylessness assumption $\eqref{eq:memoryless_definition}$ as
\[P(Y > t+s) = P(Y > s) \cdot P(Y > t)\]and notice that this describes a situation where the complementary cumulative distribution function maps addition to multiplication, which only an exponential function can do.
For discrete time, $t \in \mathbb{N}$, we can similarly obtain the same proportinality $\eqref{eq:memoryless_distribution}$ except for discrete $t$, it now describes the geometric distribution, although a different parametrization is usually used.
(All the plots here are using a distribution parametrization with expected waiting time 3 units.)
Weibull distribution
The Weibull distribution is a simple non-memoryless distribution used to model waiting times. Again, to show similary with the exponential distribution, the density of the Weibull distribution can be written as:
\[p(t|\lambda,\alpha) \propto e^{- (\lambda t)^{\alpha} + (\alpha-1)\ln(\lambda t)}\]where both $\lambda,\alpha \in \mathbb{R}^+$. From here it’s immediately obvious that it reduces to exponential distribution for
This may be useful to model some of the cases where the memorylessness is not appropriate, for example the time when a device fails considering it’s wearing off and getting less reliable as time passes.
With $\alpha<1$ it produces clusters of events occurring within a short window separated by long waiting between clusters. It’s usually meant as a continuous-time distribution, but there is a discrete variant too.
Uniform and Beta distribution
The continuous uniform distribution $U(0, \alpha)$ may be used to describe a waiting time when we know there is a certain hard limit for the event to happen no later than $t=\alpha$. I think the uniform distribution is often quite unrealistic and perhaps the more general Beta distribution would be more accurate for such hard limit cases, but given the simplicity of the uniform distribution, it may be worth it for the mathematical convenience. One may attempt to justify it by referring to the principle of maximum entropy when we actually have little knowledge about the system.
Lomax distribution
The Lomax distribution is heavy-tailed and may thus be of interest when we expect outliers in the data. (Informally that means sometimes the waiting time is extremely long.)
Waiting for $n$-th event
One thing we may ask is, given a distribution for the waiting time for one event, what’s the probability distribution of waiting for $n$ events? For example, the geometric distribution can be interpreted as follows: A salesperson is trying to sell a product and a customer will decline them with a probability given by the distribution parameter. How many times will the salesperson be declined before he sells? This is described by the geometric distribution. But now what if he needs to sell $n$ products, one to each customer?
Or similarly with the continuous time of customer purchases, each buying one piece: How long will we likely wait until we sell the entire stock of $n$ products?
There is a basic theorem with relates the sum of two random variables to the convolution. In the continuous case we have:
\[p_{X+Y}(t) = p_X(t) \ast p_Y(t) = \int_{-\infty}^{\infty} p_X(s) p_Y(t-s) \mathrm{d}s\]And there is something analogical for discrete distributions replacing the integral with a sum. Note that in our case, the lower bound of the integral could conveniently be set to $0$ rather than $-\infty$.
In particular, when we have a series of I.I.D. random variables $X_1, …, X_n$ and denote $S_n = \sum_{i=1}^n X_i$, we can write this as convolution power:
\[p_{S_n}(t) = p_{X_1}(t)^{\ast n}\]This can always be used in principle, at least with a numerical evaluation, but the integral doesn’t have an analytic solution save the few simple cases mentioned earlier. The need for numerical computation is quite impractical and may motivate choosing the simpler distributions to model the problem instead.
The notable solutions when this is possible to do analytically are summarized in the following table:
| Waiting time for one event | Waiting time for $n$-th event |
|---|---|
| Exponential | Erlang (Gamma) |
| Geometric | Negative Binomial |
| Uniform | Irwin-Hall |
| Gamma | Gamma |
Next read: Counting events